Oscilliscope Lab

The oscilliscope is a valuable tool in analyzing time varying currents. To understand these currents, we must first think of them as a sinusoidal wave or at least that they behave like one. The screen is a grid onto which the wave is projected via beaming electrons onto its surface which is cotated in phosphor and produces visible light as a result. The scope can be used to see the effects (such as DC offset) of various alterations can have on a current.

By connecting it to a function generator, the oscilliscope started to churn out the resulting graphs. The X axis represents the time and the Y axis represents the amplitude or magnitude of the current. We were able to measure both a sinusoid and a square wave (DC coupled). The last part of the lab involved measurement of two mystery signals.

Operational Amplifiers

The idea behind the op amps lab is to apply operational amplifiers in a real world scenario. There may be many instances in the real world where a circuit may be required to have a different set of voltages at different parts of it. For example, a sensor which captures certain information may not be outputting an ideal voltage for it to work with the attached processing unit. Enter the Op Amp which can make it work! The following circuit was built and all the values were recorded.



Once the circuit was constructed, it was apparent that the circuit contains a feedback loop. By putting a resistor in between the output voltage and the input voltage, the operation amplifier can be made to output the desired voltage gain.

The circuit was then connected to two separate voltage sources providing various voltages starting from 0 and ending in 1. We went in 0.25 volt increments. The following is

Vin	Vout	GAIN	Vri	Iri	Vrf
0	0	0	0	0	0
0.25	-2.39	9.958	0.24	0.235	2.39
0.5	-4.9	9.8	0.5	0.504	4.9
0.75	-7.44	9.92	0.75	0.707	7.43
1	-9.93	9.83	1.01	1	9.93

It came out that the current being drawn from sources were about 7.5 and 1.8 milliamps. These were not expected but that may be in part due to the fact that the power supplies (voltage supplies) were also being used to power the voltage dividers.

PSPICE Webassign Homework

The latest Webassign homework assignment was designed as further practice in utlilizing PSPICE to solve circuit problems. The two problems were worked out by hand first and the answers were then compared to PSPICE analysis results. The first problem was as follows;

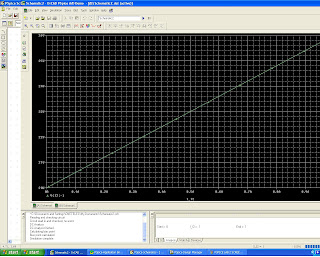
In order to solve the problem. The circuit was first constructed in PSPICE schematic with the exception of the Load being replaced with a probing current source. The idea is to run a sweep across the load with various currents (0-1 mA) with 0.1 mA increments. The results were then plotted. Here is a screenshot;

In this case, the 0-intercept (where the resistance across the load is infinite which is why the current is 0) is the Thevinin voltage while the slope of the line (voltage/current or V/I) is the Thevinin Resistance. The second problem also incorporated calculations for the maximum power displacement across the resistor. The question is as follows.

The first part of the problem was solved in the same method described for problem one. The second part of the problem involved using an actual sweeping resistance across the Resistor. The following screenshot shows the graph along with the circuit constructed in PSPICE Schematic.

With various theoretical resistances across the load, the resulting power dissipation graph was plotted so as to determine the optimum power dissipation.

Overall the results were very close to the calculated values (well within 5% which can be attributed to rounding errors). PSPICE demonstrates that there is a way with the computational power of a PC to calculate values across a circuit by setting a varying source or load and then plotting the results. The graph can then be analyzed and used to find the appropriate values. However, the PSPICE graph also gives the engineer and idea of how the circuit would operate across multiple conditions and save the engineer a lot of tedious calculations and time!

PSPICE Lab #2

The second PSPICE lab is designed to test some applications of the P SPICE engineering simulation software. The first lab was more to familiarize people with the Graphical User Interface of the program. One of the core concepts to take away from the PSPICE LAB #2 is that the program is intended to provide engineers with a quick way to design and test various designs. It would be impractical to build a prototype for every single theory or design and so P SPICE is used as an intermediate in order to separate the designs that are theoretically sound enough for Prototypes.

The Circuit on the right was created in PSPICE Schematics and involved use Viewpoints which are a neat tool to set PSPICE to display any electrical information at a point on the circuit designated by the user.

The Graph on the Right is an example of the type of graphing capabilities possible with the software. A varying voltage source which varies between 1-20 Volts at 1 Volt Increments is used as an example.

For more complex analysis involving dependent sources like the circuit on the left.

The following graph maps various factors and values.

Consequently, to figure the Norton Current, a probing voltage source is put in place of the load. The idea is to set an artificial voltage across the load and figure out the current across that voltage source.

The circuit on the left here is meant to be the thevinin representation of a more complex circuit. PSPICE can also calculate a variety of different capabilities of a given circuit including the maximum power dissipation when facing a varying load capacity.

The following power graph is a trace of the values of the power dissipated across the load at various resistance levels.










PSPICE's ability to quickly analyze a circuit with sweeping loads and source values is a valuable tool for the electrical engineer. Not only does it provide a quick way to calculate Norton and Thevinin values, it is also a way of calculating the values across a circuit under various conditions. Analysis of these graphs provide engineers with a way of seeing the best ways to implement a circuit design.

Thevinin Equivalent Lab

The Thevinin lab is designed to familiarize participants with the real life applications of Thevenin's theorem. In reality, circuits are not as simple as the ones shown for practice problems in electronic engineering classes. Thevinin's theorem allowed for every circuit no matter how complicated to be essentially be broken down into a single voltage source in series with a resistor.

The picture above shows the circuit as it was set up to be just a Thevenin equivalent circuit. Measurements were then taken.

CONFIG	THEO VALUE	MEASURED	% Error
RL2=RL2,min	8	7.68	4%
RL2=Infinite	8	8.50	8%

Overall, the percent error for the following lab was a little higher than usual. This was due to various factors such as resistors being off by +/-5%. The most expensive thing in engineering is precision and since most commercial ventures do not have an unlimited budget to purchase near perfect parts, most will try to limit error percentages by building more efficient circuits. One observation made from this lab is that reducing error in a circuit can sometimes mean using more resistors in parallel and series to minimize error by spreading it out among multiple components instead of gambling on one.

PSpice Tutorial: Part 1 Introduction and DC Analysis

As the name suggests, the lab was our first foray into the wonderful world of PSpice, a simulation tool for electrical circuits. In its latest iteration, PSpice is outfitted with a cutting edge GUI which makes use simple, even for lowly ENGR 44 students!

Once the program has been installed, the first order of business was to add certain libraries which were included. The default libraries include typical beginning electrical circuit stuff and I suspect that there are advanced libraries out there with all manner of objects to be inserted into an electrical circuit.

After adding the required libraries, we then proceeded to create a new project and after navigating multiple menus, we arrived at the final dashboard for a PSpice project. The most important thing about these PSpice schematics is to be careful in drawing the wires and objects. Many people in the class got errors when trying to run their simulations (myself included) due to wiring nodes that shouldnt exist and etc. Upon successful completion of a schematic and a simulation run, the following screen should appear.

It should also be noted that PSpice REQUIRES the setting of a GROUND to compute all other values relative to that point. Once complete, the simulation should display all calculated voltages at different points in the circuit. It will also display currents!

The following HW problem was made extremely easy with the application of PSpice. Needless to say, PSpice is an invaluable tool to an electrical engineer (or student of).

Nodal Analysis Lab

The Nodal Analysis Lab was designed to familiarize students with real world applications of the Node Voltage Technique. The idea behind it is to build a system which can sustain damage to one part of the circuit without bringing everything offline which has obvious uses in the real world. One simple way to think about how such a task is accomplished is the use of multiple voltage sources and loads. To test this out, students built the following circuit;

 

The following circuit is composed of several resistors which are meant to simulate the loads on a real world circuit. The values of the resistors starting from the left are; 100 , 1000, 220, 1000, and 220 Ohms. They are connected together in several nodes with power supplied from the left and right sides from two separate power supplies. Before building the circuit, students first calculated the theoretical values for the power supplies needed. Using the nodal equations, students were then able to calculate both the corresponding currents and power supplied by both batteries. 

 

Students simply used a 12 and 9 Volt setting respectively. The following is the measured values compared to actual values used.

Component	Nominal Value	Measured Value	Power or Current Rating
R1 (Ohms)	100	99	0.25 W
R2 (Ohms)	220	224	0.25 W
R3 (Ohms)	220	218	0.25 W
RL1 (Ohms)	1000	983	0.25 W
RL2 (Ohms)	1000	989	0.25 W
Vbat1 (Volts)	12	12.12	2 Amps
Vbat2 (Volts)	9	9.09	2 Amps

Here were the measurements taken when compared to the theoretical values.

Component	Nominal Value	Measured Value	% Error
Ibat1	17.5 mA	17.39 mA	0.63%
Ibat2	1.5 mA	1.5 mA	0%
V2	10.25 V	10.35 mA	0.98%
V3	8.67 V	8.75 mA	0.91%

As you can see, the experiment went very smoothly and nothing surpassed 1% error. A system with 2 separate power supplies can remain at least partially function if one is disabled. This measure of reliability is critical to real world applications in which electronic circuits may be subjected to the elements, or a copper tipped explosively formed penetrator punching its way through a military electronics system. By supplying two voltage sources, a system's operational capacity is not bottle necked at simply knocking out the voltage supply. In fact, by varying the voltage settings of the sources, the system can be controlled as demonstrated by the final portion of the lab. In order to get 0 current going across the RC2, a voltage of 9.9 V and 10.98 V are needed for VS1 and VS2 respectively.

Voltage Dividers Lab

The Voltage Dividers Lab is designed to familiarize engineers with the concept of an electrical system having multiple loads that can be switched on and off. One very basic example of this is an electrical fan with multiple speed settings. The idea is to provide multiple loads across a circuit and in this case use it to control the current going through any individual load.

The picture (courtesy of Nick Moran's Blog)  illustrates the basic concept of the circuit. Imagine a Voltage supply and resistor (resistor box) is connected in series with 3 resistors of the same resistance value in parallel to each other. These resistors would then be either connected or disconnected to modify the current going through any of them. In a real world example, one of these resistors could be replaced with the load and voila; simple way to vary the current across a load!

Here is the data we collected with varying configurations of resistors in parallel;

Config	EQ Resistance (Ohms)	VBUS (Volts)	IBUS (mA)	P Load (calculated Watts)
1 Load	1003	5.68	5.72	0.032
2 Loads	499	5.34	10.76	0.06
3 Loads	334	5	15.25	0.076

Overall the circuit tested in this voltage divider lab is a great way to control currents through a given system without being needlessly complex. The real world applications of this concept are numerous and can be found in countless modern circuits. Quite counter intuitively, the more loads placed in parallel, the less the equivalent resistance and hence the less strain on a battery because it would have to supply less current!

Introduction to Biasing

This lab consisted of 2 Light Emitting Diodes connected in parallel to each other to a current source. Unfortunately, the LEDs were not rated high enough to be able to withstand the kind of voltage being put out by a 9 V battery (simulated in this case by a power supply) so we had to connect two resistors (one before each LED) to lower the voltage. Here is the basic set-up that follows;

Current enters from the orange wire on the top right corner of the bread board, it is then split among 2 resistors and the resulting currents go through the respective resistors and into the LEDs (using the correct resistors we were able to ensure that the LEDs did not blow) and then back into the power supply through the green (right) and yellow wires. The other orange and green wires on the left were connected to the voltmeter

The red LED was rated to take 2V while the yellow LED was rated to take 5V. Unfortunately, the power supply puts out 9V so we had to put a resistor before each LED. Using Ohm's Law we were able to calculate the equivalent resistances of the LEDs which gave us the ratio of the current going through each. After knowing the currents going through each branch and the maximum voltage of the LEDs we were able to calculate the values of the resistors which were 175.8 Ohms and 350 Ohms for 1 and 2 respectively

Introduction to DC Circuits

The Introduction to DC Circuits Lab started off with a simple concept pictured below.

Real world application must take into account the natural resistivity of the material that conducting cables are made of.

In this set up, a current flows from the battery through the cable to the "load" then back to the battery again. In a perfect world, all resistance in this system would come from the load and up until now we've taken for granted that all theoretical cables are perfect conductors. The real world is not as forgiving however, and cables themselves (regardless of material) have inherent resistances.

Starting with the red cable (farthest right): Current flows from DC power supply to a resistor box then into a current meter and then into a 1000 Ohm resistor (which simulates the load). The voltage across the resistor is also measured by a voltmeter.

This comes into play when designing real life applications that require current to be transported over long distances; the conductivity and resistance of the material must be accounted for because it will make a difference in the overall system. To demonstrate this, we set up the following lab (pictured on the right).

What we found (aside from the fact that none of the equipment outputted the exact amounts stated on its labels; I.E 12V power supply actually put out 12.18V) was that there is a maximum length that exists for which the current could not effectively carried past that.